Recurrent Model of Visual Attention
In this blog post, I want to discuss how we at Element-Research implemented the recurrent attention model (RAM) described in [1]. Not only were we able to reproduce the paper, but we also made of bunch of modular code available in the process. You can reproduce the RAM on the MNIST dataset using this training script. We will use snippets of that script throughout this post. You can then evaluate your trained models using the evaluation script.
The paper describes a RAM that can be applied to image classification datasets.
The model is designed in such a way that it has a bandwidth limited sensor of the input image.
As an example, if the input image is of size 28x28 (height x width),
the RAM may only be able to sense an area of size 8x8 at any given time-step.
These small sensed areas are refered to as glimpses.
SpatialGlimpse
Actually, the paper’s glimpse sensor is little bit more complicated than what we described above, but nevertheless simple. Keeping in step with the modular spirit of Torch7’s nn package, we created a SpatialGlimpse module.
module = nn.SpatialGlimpse(size, depth, scale)
Basically, if you feed it an image, say the classic 3x512x512 Lenna image:

And you run this code on it:
require 'dpnn'
require 'image'
img = image.lena()
loc = torch.Tensor{0,0} -- 0.0 is the center of the image
sg = nn.SpatialGlimpse(64, 3, 2)
output = sg:forward{img, loc}
print(output:size()) -- 9 x 64 x 64
-- unroll the glimpse onto its different depths
outputs = torch.chunk(output, 3)
display = image.toDisplayTensor(outputs)
image.save("glimpse-output.png", display)
You will end up with the following (unrolled) glimpse :

While the input is a 3x512x512 image (786432 scalars),
the output is very small : 9x64x64 (36864 scalars), or about
5% the size of the original image.
Since the glimse here has a depth=3 (i.e. it uses 3 patches),
each successive patch is scale times the size of the prevous one.
So we end up with a high-resolution patch of a small area,
and successively lower-resolution (i.e. downscaled) patches of larger areas.
This carries fascinating parallels to how our own human attention mechanism may possibly work.
Quite often, we humans can vividly see the details of what we focus our attention on,
while nevertheless maintaining a blurry sense of the outskirts.
Although not necessary for reproducing this paper,
the SpatialGlimpse can also be partially backpropagated through.
While the gradient w.r.t. the img tensor can be obtained,
the gradients w.r.t. the location (i.e. the x,y coordinates of the glimpse) will be zero.
This is because the glimpse operation cannot be differentiated w.r.t. the location.
Which brings us to the main difficulty of attention models :
how can we teach the network to glimpse at the right locations?
REINFORCE algorithm
Some attention models use a fully differentiable attention mechanism, like the recent DRAW paper [2]. But the RAM model uses a non-differentiable attention mechanism. Specifically, it uses a the REINFORCE algorithm [3]. This algorithm allows one to train stochastic units through reinforcement learning.
The REINFORCE algorithm is very powerful as it can be used to optimize stochastic units (conditioned on an input), such that they minimize an objective function (i.e. a reward function). Unlike backpropagation [4], this objective need not be differentiable.
The RAM model uses the REINFORCE algorithm to train the locator network :
-- actions (locator)
locator = nn.Sequential()
locator:add(nn.Linear(opt.hiddenSize, 2))
locator:add(nn.HardTanh()) -- bounds mean between -1 and 1
locator:add(nn.ReinforceNormal(2*opt.locatorStd)) -- sample from normal, uses REINFORCE learning rule
locator:add(nn.HardTanh()) -- bounds sample between -1 and 1
locator:add(nn.MulConstant(opt.unitPixels*2/ds:imageSize("h")))
The input is the previous recurrent hidden state h[t-1].
During training, the output is sampled from a normal
distribution with fixed standard deviation.
The mean is conditioned on h[t-1] through an affine transform (i.e. Linear module).
During evaluation, instead of sampling from the distribution, the output is taken to be the input, i.e. the mean.
The ReinforceNormal module
implements the REINFORCE algorithm for the normal distribution.
Unlike most Modules, ReinforceNormal ignores the gradOutput when backward is called.
This is because the units it embodies are in fact stochastic.
So then how does it generate gradInputs when the backward is called?
It uses the REINFORCE algorithm, which requires that a reward function be defined.
The reward used by the paper is very simple, and yet not differentiable (eq. 1) :
R = I(y=t)
where R is the raw reward, I(x) is 1 when x is true and 0 otherwise
(see indicator function),
y is the predicted class, t is the target class.
Or in Lua :
R = (y==t) and 1 or 0
The REINFORCE algorithm requires that we differentiate the probability density or mass function (PDF/PMF) of the distribution w.r.t. the parameters. So given the following variables :
f: normal probability density functionx: the sampled values (i.e.ReinforceNormal.output)u: mean (inputtoReinforceNormal)s: standard deviation (ReinforceNormal.stdev)
the derivative of log normal w.r.t. mean u is :
d ln(f(x,u)) (x - u)
------------ = -------
d u s^2
So where does d ln(f(x,u,s) / d u fit in with the reward?
Well, in order to obtain a gradient of the reward R w.r.t.
to input u, we apply the following equation (eq. 2, i.e. the REINFORCE algorithm):
d R d ln(f(x,u))
--- = a * (R - b) * --------------
d u d u
where
a(alpha) is just a scaling factor like the learning rate ; andbis a baseline reward used to reduce the variance of the gradient.fis the PMF/PDFuis the parameter w.r.t. which you want to get a gradientxis the sampled value.
In the paper, they take b to be the expected reward E[R].
They approximate the expectation by making b a (conditionally independent) parameter of the model .
For each example, the mean square error between R and b is minimized by
backpropagation. The beauty of doing this, instead of,
say, making b a moving average of R, is that the baseline reward b
learns at the same rate as the rest of the model.
We decided to implement the reward = a * (R - b) part of eq. 2
within a VRClassReward criterion,
which also implements the paper’s varianced-reduced classification reward function (eq. 1):
vcr = nn.VRClassReward(module [, scale, criterion])
The nn package was primarily built for backpropagation, so we had to find a not-too-hacky way of
broadcasting the reward to the different
Reinforce modules.
We did this by having the criterion take the module as argument,
and adding the Module:reinforce(reward)
method. The latter allows the Reinforce modules (like ReinforceNormal) to
hold on to the criterion’s broadcasted reward for later. Later being when backward is called
and the Reinforce module(s) compute(s) the gradInput
(i.e. d R / d U) using the REINFORCE algorithm (eq. 2).
And then nn is happy, because with the gradInput, it can continue
the backpropagation from the Reinforce module to its predecessors.
So to summarize, if you can differentiate the PMF/PDF w.r.t. to its parameters, then you can use the REINFORCE algorithm on it. We have already implemented modules for the categorical and bernoulli distributions :
Recurrent Attention Model
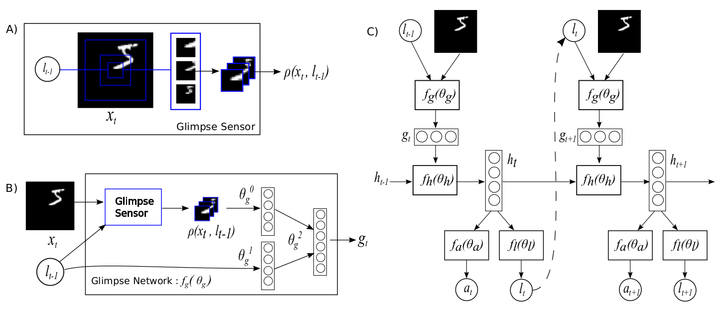
Okay, so we discussed the glimpse module and the REINFORCE algorithm, lets talk about the recurrent attention model. We can divide the model into its respective components :
The location sensor. Its inputs are the x, y coordinates of the current glimpse location,
so the network knows where its looking at each time-step :
locationSensor = nn.Sequential()
locationSensor:add(nn.SelectTable(2))
locationSensor:add(nn.Linear(2, opt.locatorHiddenSize))
locationSensor:add(nn[opt.transfer]())
The glimpse sensor is what it’s looking at :
glimpseSensor = nn.Sequential()
glimpseSensor:add(nn.DontCast(nn.SpatialGlimpse(opt.glimpsePatchSize, opt.glimpseDepth, opt.glimpseScale):float(),true))
glimpseSensor:add(nn.Collapse(3))
glimpseSensor:add(nn.Linear(ds:imageSize('c')*(opt.glimpsePatchSize^2)*opt.glimpseDepth, opt.glimpseHiddenSize))
glimpseSensor:add(nn[opt.transfer]())
The glimpse network is where the glimpse and location sensor mix through a hidden layer to form the input layer of the Recurrent Neural Network (RNN) :
glimpse = nn.Sequential()
glimpse:add(nn.ConcatTable():add(locationSensor):add(glimpseSensor))
glimpse:add(nn.JoinTable(1,1))
glimpse:add(nn.Linear(opt.glimpseHiddenSize+opt.locatorHiddenSize, opt.imageHiddenSize))
glimpse:add(nn[opt.transfer]())
glimpse:add(nn.Linear(opt.imageHiddenSize, opt.hiddenSize))
The RNN is the where the glimpse network and the recurrent layer come together.
The output of the rnn module is the hidden state h[t] where t indexes the time-step.
We used the rnn package to build it :
-- rnn recurrent layer
recurrent = nn.Linear(opt.hiddenSize, opt.hiddenSize)
-- recurrent neural network
rnn = nn.Recurrent(opt.hiddenSize, glimpse, recurrent, nn[opt.transfer](), 99999)
We have already seen the locator network above, but here it is again :
-- actions (locator)
locator = nn.Sequential()
locator:add(nn.Linear(opt.hiddenSize, 2))
locator:add(nn.HardTanh()) -- bounds mean between -1 and 1
locator:add(nn.ReinforceNormal(2*opt.locatorStd)) -- sample from normal, uses REINFORCE learning rule
locator:add(nn.HardTanh()) -- bounds sample between -1 and 1
locator:add(nn.MulConstant(opt.unitPixels*2/ds:imageSize("h")))
The locator’s task is to sample the next location l[t] (or action)
given the previous hidden state h[t-1], i.e. the previous output of the rnn.
For the first step, we use h[0] = 0 (a tensor of zeros) for the previous hidden state.
We should also bring your attention to the opt.unitPixels variable,
as it is very important and not specified in the paper.
This variable basically outlines how far (in pixels) near the borders the
center of each glimpse can reach with respect to the center.
So a value of 13 (the default) means that the center of the glimpse can
be anywhere between the 2rd and 27th pixel (for a 1x28x28 MNIST example).
So glimpses of the corner will have fewer zero-padding values then if opt.unitPixels = 14.
We need to encapsulate the rnn and locator into a module that would
capture the essence of the RAM model.
So we decided to implement a module that took the full image as input,
and output the sequence of hidden states h.
As its name implies, this module is a general purpose
RecurrentAttention module :
attention = nn.RecurrentAttention(rnn, locator, opt.rho, {opt.hiddenSize})
It’s so general-purpose that you can use it with an
LSTM module,
and different glimpse or locator modules. As long as these respectively preserve
the same {input, action} -> output interfaces (glimpse) and use the REINFORCE algorithm (locator), of course.
Next we build an agent by stacking a classifier on top of the RecurrentAttention module.
The classifier’s input is the last hidden state h[T],
where T is the total number of time-steps (i.e. glimpses to take):
-- model is a reinforcement learning agent
agent = nn.Sequential()
agent:add(nn.Convert(ds:ioShapes(), 'bchw'))
agent:add(attention)
-- classifier :
agent:add(nn.SelectTable(-1))
agent:add(nn.Linear(opt.hiddenSize, #ds:classes()))
agent:add(nn.LogSoftMax())
You might recall that the REINFORCE algorithm requires a baseline reward b?
This is where that happens (yes, it requires a little bit of nn kung-fu):
-- add the baseline reward predictor
seq = nn.Sequential()
seq:add(nn.Constant(1,1))
seq:add(nn.Add(1))
concat = nn.ConcatTable():add(nn.Identity()):add(seq)
concat2 = nn.ConcatTable():add(nn.Identity()):add(concat)
-- output will be : {classpred, {classpred, basereward}}
agent:add(concat2)
At this point, the model is ready for training.
The agent instance is effectively the RAM model detailed in the paper.
Training
Training is pretty straight-forward after that. The script can be launched with the default hyper-parameters. It should take 1-2 runs to find a validation minima that reproduces the MNIST test results of the paper. We are still working on reproducing the Translated and Cluttered MNIST results.
Results
In the paper, they get 1.07% error on MNIST with 7 glimpses. We got 0.85% error after 853 epochs of training (early-stopped on the validation set of course). Here are some glimpse sequences. Note how the first frames start at the same location :

And this is what the model sees for those sequences:
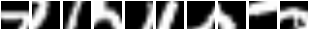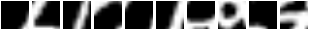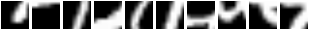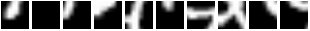
So basically, REINFORCE did a good job of teaching the module to focus its attention on different regions given different inputs. A failure mode (bad) would have been to see the model do this :

In that particular case, the opt.unitPixels was set to 6 instead of 12
(so the attention was limited to a small region in the center of the image).
You don’t want this to happen because it means the attention is conditionally independent of the input (i.e. dumb).
Here are some results for the Translated MNIST dataset :

For this dataset, the images are of size 1x60x60 where each image contains a randomly placed 1x28x28 MNIST digit.
The 3x12x12 glimpse uses a depth of 3 scales
where each successive patch is twice the height and width of the previous one.
After 683 epochs of training on the Translatted MNIST dataset, using 7 glimpses, we obtain 0.92% error.
The paper reaches 1.22% and 1.2% error for 6 and 8 glimpses, respectively.
The exact command used to obtain those results:
th examples/recurrent-visual-attention.lua --cuda --dataset TranslatedMnist --unitPixels 26 --learningRate 0.001 --glimpseDepth 3 --maxTries 200 --stochastic --glimpsePatchSize 12
Note : you can evaluate your models with the evaluation script. It will generate a sample of glimpse sequences and print the confusion matrix results for the test set.
Conclusion
This blog discussed a concrete implementation of a Recurrent Model for Visual Attention using the REINFORCE algorithm. The REINFORCE algorithm is very powerful as it can learn non-differentiable criterions through reinforcement learning. However, like many reinforcement learning algorithms, it does take a long time to converge. Nevertheless, as demonstrated here and in the original paper, the ability to train a model to learn where to focus its attention can provide significant performance improvements.
References
- Volodymyr Mnih, Nicolas Heess, Alex Graves, Koray Kavukcuoglu, Recurrent Models of Visual Attention, NIPS 2014
- Gregor, Karol, et al., DRAW: A recurrent neural network for image generation, Arxiv 2015
- Williams, Ronald J., Simple statistical gradient-following algorithms for connectionist reinforcement learning, Machine learning 8.3-4 (1992): 229-256.
- Rumelhart, David E., Geoffrey E. Hinton, and Ronald J. Williams. Learning internal representations by error propagation, No. ICS-8506